Anything you try to improve will have a growth curve. Imagine you ran everyday and you tracked your speed to finish a 5-mile course. Smoothing out the noise, over enough time you’d probably get a graph like this:
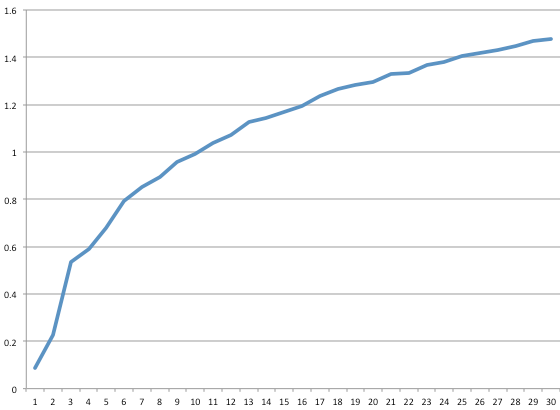
Here, improvement works on a logarithmic scale. As you get better, it gets harder and harder to improve. Elite athletes expend enormous effort to shave seconds off their best times. Novice athletes can shave minutes with just a little practice.
Logarithmic growth is the first type of growth. This is where you see a lot of progress in the beginning, but continuing progress is more difficult.
Now imagine a different graph. This time you’ve build a new website you update regularly and you’re measuring subscribers. This graph would likely look very different:
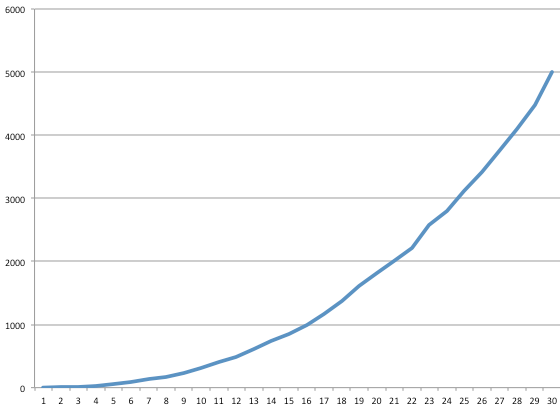
This is exponential growth, the second type of growth. Website traffic is often exponential because as a blog attracts more readers, there are more opportunities for word about the blog to spread. A blog with zero traffic also has zero word of mouth.
I’ve noticed most things tend to be either logarithmic or exponential growth. Despite this, linear progress is what most people expect. We tend to expect things to move in the same direction or rate as they have in the past. This violation of our expectation leads to some mistakes in how we set goals and act on them.
The Logarithmic Growth Mistake
The first kind of mistake is assuming straight-line growth, when reality is actually logarithmic. There are many situations which usually fit this pattern:
- Athletic performance
- Weight gain/loss
- Learning a new language
- Productivity
- Mastery of a complex skill
Assuming straight-line growth means overconfidence in long-term progress. As a result, it is easy to hit plateaus if the difficulty isn’t deliberately tuned to break your comfortable rhythm.
Logarithmic growth also implies it is easier to slide back down the hill. Since it is so steep in the beginning, carelessness can mean those immediate gains are often easily lost. Losing weight quickly may be more desirable than losing it slowly, but it also risks putting it back on again quickly if you stop your efforts.
Logarithmic mistakes are common, but so to are mistakes when reality is in the other type of growth curve.
The Exponential Growth Mistake
Once again, people view progress linearly when it is, in fact, exponential. Some examples which usually follow exponential curves for at least part of their lifecycle are:
- Technological improvement (e.g. Moore’s Law)
- Business growth
- Wealth
- Rewards to talent/career
Unlike logarithmic curves, almost nothing is consistently exponential. Most are only exponential over some range of values, outside of which they are logarithmic again.
No business reaches near-infinite values, even though this would be implied by an exponential curve. Eventually market share is saturated or competition stabilizes growth. However, for many types of businesses, exponential growth can persist for much of the business lifecycle.
Exponential curves are somewhat rarer than logarithmic ones, however the mistakes here can be even more costly. Expecting linear growth when it is actually exponential causes many people to give up way before they should.
Several years ago, I remember being disheartened when drawing straight-line projections of my business income. At the going rates, it was often a dozen years away or more before I could make a full-time living at it. However, my income turned out to be exponential. Despite spending more time below my ideal projections, I ended up eventually surpassing them.
Exponential areas of life are full of quitters. People making linear assessments of viability and giving up before the exponential curve can take hold. Not all of this is irrational, many exponential areas are high-variance as well. However, the problem with exponential domains is that the feedback can often look bad, even when it is good.
Is Your Growth Exponential or Logarithmic?
Both types of mistakes, failing to recognize exponential domains and logarithmic ones, are costly. It’s not always clear which is which, but by reasoning about the features of a domain you can get a better sense which one it is likely to be.
The easiest way to tell is to look at how other people have progressed in that field. Don’t pay attention to their rates, just pay attention to the shape of their growth trajectory. Is it the kind that slows down with mastery or speeds up?
Exponential growth stories tend to be the ones where a person struggled long and hard with little to show for it, then started quickly gaining success. These stories often seem to be overnight successes, since they ignore the years of obscure toiling.
Logarithmic growth stories involve a continuous dedication to remaining at your peak. A fluent speaker of a second language will comment on the regular practice required, not the sudden moment where it all “happened”.
Other features of the environment can tell you whether something is exponential or logarithmic. Exponential environments often seem to be based on a catch-22 or circular causality. Having money makes it much easier to make more money, not only because of interest rates but because people give rich people opportunities they wouldn’t to those without success.
Logarithmic domains usually have diminishing returns once the “obvious” solutions are taken. The more you work at them, the harder you have to look for insight to generate new gains. Occasionally you can discover overlooked opportunities and regain the steep part of the curve, but this is inherently difficult.
Growth Mindsets
In logarithmic domains, two mindsets are important. In the beginning, high-growth phase, the emphasis needs to be on maintaining long-term habits. Since growth is fast initially, care needs to be taken so that it won’t slide back down once effort is removed.
In the later, low-growth phase, the emphasis needs to be on habit breaking. Since low-growth is often caused by calcifying routines, deliberate effort needs to be taken to break out of that comfort zone.
In exponential domains, the mindset of resilience and endurance are critical. Since feedback is sparse and generally negative during the initial part of the curve, it takes dedication to persist. Part of the reason, entrepreneurs are often consumed by their own vision is that it helps block out the negative feedback until they can reach the exponential part of their growth.
Now it’s your turn. What are you working on right now? Is it more exponential or logarithmic? What features of your environment do you believe make it that way? Share your thoughts in the comments.


 I'm a Wall Street Journal bestselling author, podcast host, computer programmer and an avid reader. Since 2006, I've published weekly essays on this website to help people like you learn and think better. My work has been featured in The New York Times, BBC, TEDx, Pocket, Business Insider and more. I don't promise I have all the answers, just a place to start.
I'm a Wall Street Journal bestselling author, podcast host, computer programmer and an avid reader. Since 2006, I've published weekly essays on this website to help people like you learn and think better. My work has been featured in The New York Times, BBC, TEDx, Pocket, Business Insider and more. I don't promise I have all the answers, just a place to start.