Useful Mental Model: Exponential Growth

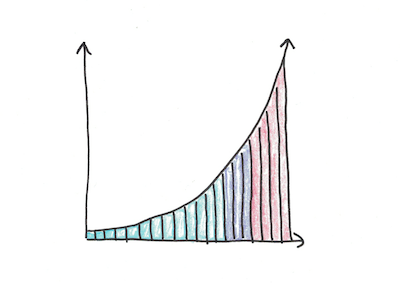
Some ideas are so powerful and useful, that once you understand them deeply you start to see them everywhere. One of those ideas is exponential growth.

Exponential growth occurs in many systems, from animal populations to investment accounts. Our brains don’t seem very apt for reasoning exponentially. Instead, we tend to extrapolate things in ways that consistently underestimate how big exponential growth eventually gets.

That being said, true, undamped exponential growth rarely lasts forever. A rabbit population that doubles every six months would, in theory, fill the entire planet under a layer of rabbits miles thick in no time at all.

Yet we’re not all swimming in rabbits, so exponential growth tends to have limits. Understanding those limits is at least as important as understanding the underlying growth itself.

What is Exponential Growth?

Mathematically, exponential growth occurs whenever the speed something increases proportionally to how much there is at any moment.

The proportionality of growth to amount, is what leads to the great result from calculus, that the exponential function (to the base of e) is its own derivative. Growth = Quantity.

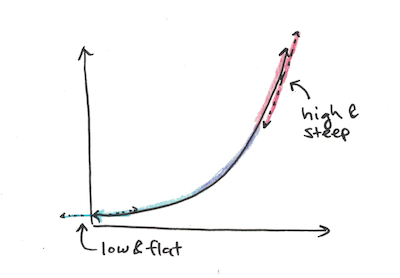
Qualitatively, exponential functions grow really fast.

In fact, if you take an exponential function out long enough, it eventually gets bigger than any finite polynomial. Polynomials are functions that take a quantity and square it, cube it, or raise it to any finite power. Even f(x) = x^12345 will eventually be smaller than an exponential function.

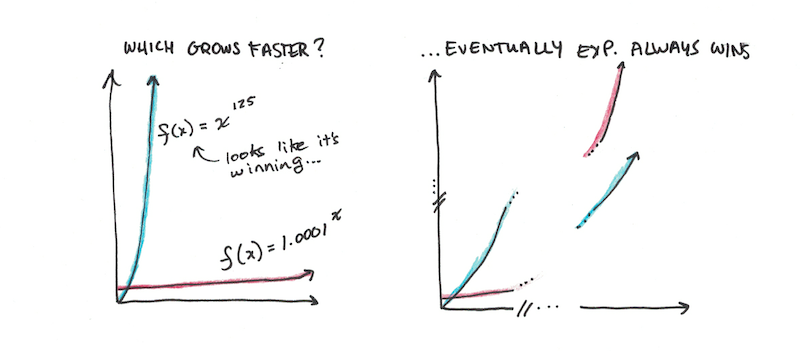
This fact about exponentials means that we often fail to predict just how large they will get. Even minuscule starting amounts and slow growth rates can start growing tremendously, if you give them enough time.

Where Do We See Exponential Growth?

True exponential growth occurs when the growth depends in some way on the amount you currently have.

Money in interest-earning accounts is a clear example. The amount of money you earn depends directly on the amount that is already in the account. That proportionality means you have exponential growth.

Populations of rabbits, where each pair of bunnies can make more babies, will also grow exponentially since the amount the population can grow depends on the amount that’s already there.

Exponential growth can also occur in other domains. Many businesses have exponential growth curves (at least for awhile) because being bigger gives proportionally more opportunities to get even bigger.

My friend James Clear likes to argue that habits are the exponential growth of personal improvement. Get 1% better every day, and you quickly get a lot better overall. It’s clear, like the start-ups or the rabbits, that such growth can’t go on forever, but there’s probably places where consistent small improvements really do compound.

Where Don’t You See Exponential Growth?

Not everything grows exponentially, so why not? As I’ve said in other lessons on this series of useful mental models, it’s at least as important to recognize when a pattern doesn’t match as when it does.

Exponential growth fails to apply when there is no longer a proportionality between the amount and the growth. For instance, fitness isn’t exponential growth because your improvement (in weight loss, pushups or running time) actually slows as you get better.

Similarly, you may experience exponential growth for awhile, and then other constraints may drop you out of exponential growth. If you’re a new business owner, each new opportunity exposes your business to new people, which fuels more growth. However, at a certain point, you may not be able to effectively handle all the new opportunities. As some go to waste, you drop out of exponential growth because future growth brings fewer opportunities you actually act on.

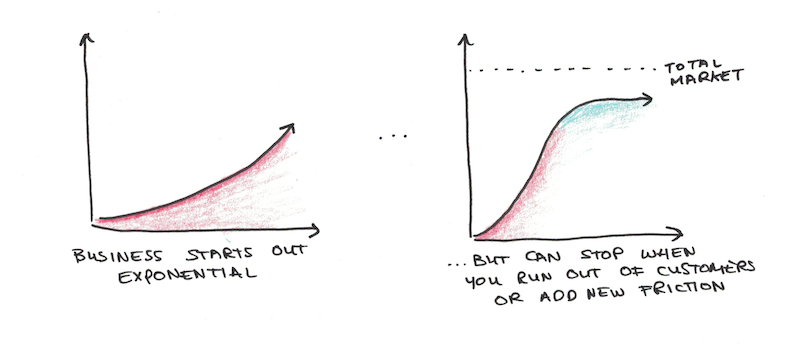
That sustained perpetual exponential growth almost never occurs is an important feature of exponential growth. All of our models of reality tend to be approximations. Because exponential growth reaches such enormous heights, considerations that were unimportant when the total amount was small eventually become very important.

At low amounts of gravity, Newton’s laws apply. At high amounts, space and time warp and you need Einstein. Those corrections are minuscule when dealing with everyday things, but if the Earth had exponentially growing mass, you’d have to quickly start worrying about those things.

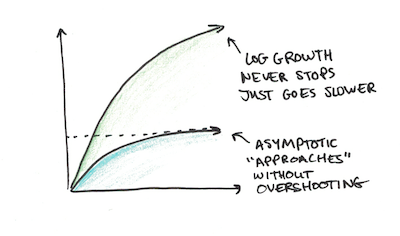
A common pattern to look for as well, therefore, is one where exponential growth shifts into logarithmic or asymptotic growth. Logarithmic growth can continue forever, but it gets slower proportional to the amount, the opposite of exponential growth. Asymptotic growth will get closer and closer to a maximum value.

Friction, side-effects, waste and loss all usually make exponential curves hit a limit.

Money tends to be an exception to this, only insofar as few of us accumulate enough wealth for the exponential growth nature of money to stop being true. However, if you had a bank account accumulating interest for ten thousand years, it might become a substantial fraction of the economy, at which point who can really say whether you (or your descendants) could actually keep it from being broken up or stolen.

Applying Lessons of Exponential Growth

The first way to use this mental model is to learn to spot it. If you think a situation might have exponential growth, ask yourself, does an increase in the amount cause a proportional increase in the growth?

If it does, then you should consider that your naive extrapolations will likely underestimate how much growth you’re likely to experience. Exponential curves are hard to imagine, and so most people make linear extrapolations, even when those aren’t the best fit.

At the same time, be wary of assuming exponential curves will go on forever. They rarely do, either because they become so big that friction and waste start to slow them down, or because they’re only exponential across some limited range, switching back to slower growth curves or stopping entirely.