In case you missed it, I spent last month learning MIT’s quantum mechanics. I’ve written a bit about how the project went, what I did and why I did it here. Today, I’d like to talk about what I’ve learned and try to explain, without using math, what picture of reality quantum mechanics gives us about the world.
Trying to explain quantum mechanics, as a non-physicist, is a risky operation. Few topics attract more nonsense and pseudoscience than popularizations of quantum mechanics. I really don’t want to add to that pile of garbage.
Still, after spending some time intensely learning the subject, I figured it would be useful to share what I’ve learned, to try to show why I think it was worthwhile to learn in the first place. Therefore, if you have the interest to keep reading, think of this as a summary of my experience, rather than an authoritative guide to quantum mechanics.
If you really do what an authoritative guide to quantum mechanics, you have two good options.
- The first is to watch Richard Feynman’s brilliant lectures which describe, without any math harder than squaring a number, how quantum mechanics works.
- If you want to go deeper, as I did, then I recommend also taking MIT’s free 8.04 class in quantum physics. To understand it, you’ll need to have taken calculus up to differential equations at least, and studied classical mechanics, electromagnetism and wave mechanics.
Those caveats and risks aside, here’s my intuitive understanding of how quantum mechanics works (minus the math).
How Reality Really Is
Quantum mechanics may sound like a weird, esoteric theory. But the amazing thing is, that it is the best possible model physicists have found for describing pretty much all the stuff in existence. Light, electrons, atoms and even you and I are governed by quantum mechanics. Even gravity, which physicists haven’t yet unified with quantum mechanics, is suspected to have a quantum theory at its core, so it’s a really general idea.
Not only is quantum mechanics nearly universal, it’s also super accurate and successful. The difference between experiment and prediction is insanely high (Richard Feynman compares the two by saying it’s like measuring the distance between the Earth and Moon and being off by only a foot). Thus, weird as it is, quantum mechanics is a better candidate for “how stuff really is” than anything else we have dreamt up.
Okay, so the near-universality and success of the theory out of the way, what does it actually say about the world?
One way to describe it is to say that all stuff can be modeled by a wavefunction. Wavefunctions aren’t too complicated, they’re a lot like waves you’re used to. If you took water waves in the open ocean, and measured the height at each point, you could probably graph something that looks like a wavefunction.
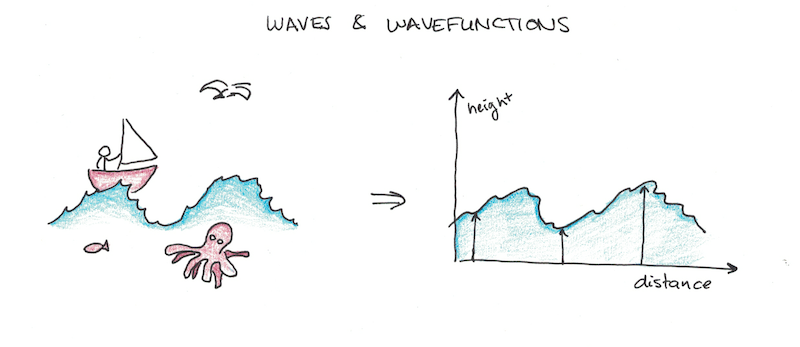
There’s a lot of connections between waves of water and quantum wavefunctions which can make (some) of the quantum weirdness seem rather ordinary. Consider the famous Uncertainty Principle, which says you can’t simultaneously know the position and momentum of a particle.
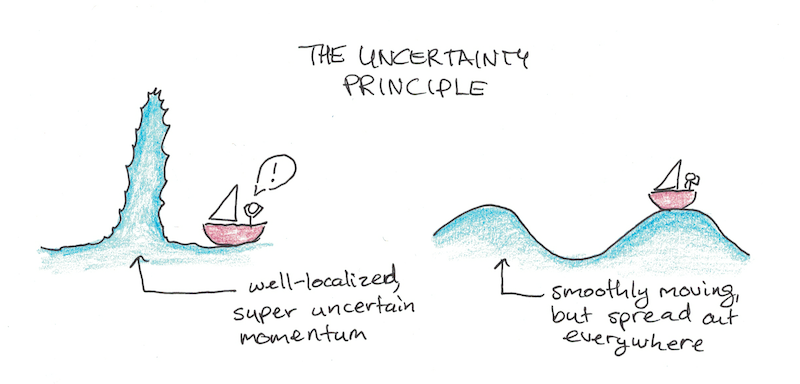
There’s something analogous in water waves. To make a wave really well localized (meaning all the water is bunched up in one place), you have to make it very unstable. To make it move at a uniform speed, you need to spread it out into regular crests and troughs. Therefore, definite position or momentum, both can’t exist simultaneously because those things mean contradictory things when we’re talking about waves.
What’s Weird About Waves?
If wavefunctions were just waves like water, though, while they may be a bit tricky to calculate, they wouldn’t be weird. Physicists have dealt with waves for centuries, and it’s not so hard to understand.
Instead, wavefunctions add two new properties which are very strange:
- Instead of just having one value at every point, wavefunctions have two. While a water wave can be represented by knowing its height at each point, the wavefunction actually has an arrow at each point. These aren’t real arrows (for instance, they stay two-dimensional, even when we deal with 3D situations) but they indicate that there’s more going on than in simple water waves. The fact that the wavefunction is made of arrows instead of values has some surprising implications, which I’ll explain later.
- Wavefunctions aren’t waves of stuff, the way that waves on the ocean are waves of water. Instead wavefunctions are waves of probability. Here, it’s the (squared) length of the arrow at each point that says how likely it is that you’ll find the particle there. A big swell in your wavefunction means your particle is more likely (although not guaranteed) to be found there.
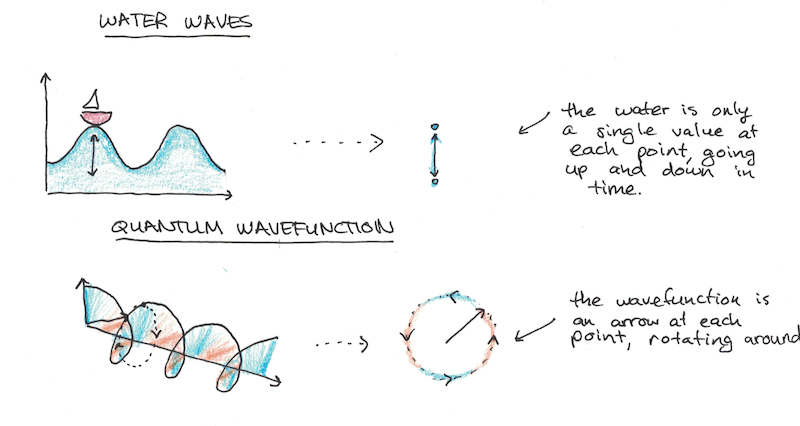
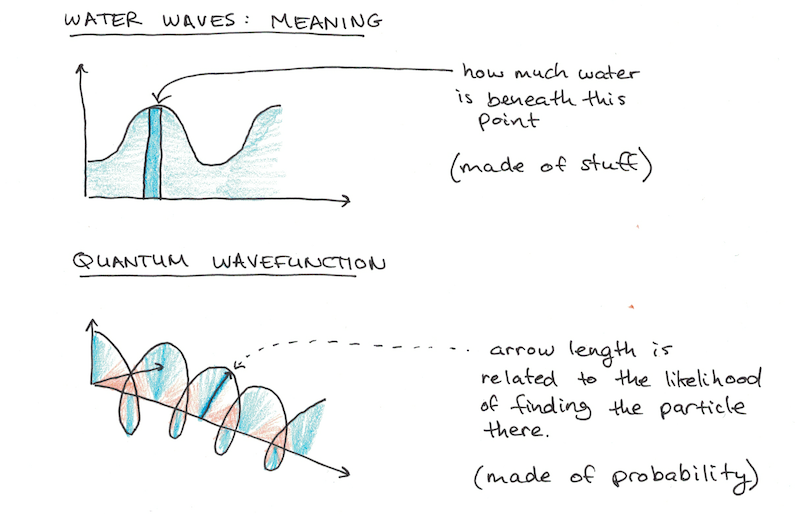
These two strange facts result in a lot of surprising implications for quantum mechanics which are nothing like regular waves which have only one value at each point and are made of stuff, not probability.
Arrows and Probability Waves
The first strange idea has to do with superposition. This is a fancy term that basically means adding, and it is one with a classical analogy: if you make ripples on water in one place, and ripples on water in a different place, they will stack on top of each other when they meet, but otherwise pass through each other unaffected.
This is a neat property of waves which helps with analyzing them since you can break down a complicated wavefunction into different superposition states to make the analysis tractable. However, from a purely visualizable perspective, I often find it easier to just imagine the wavefunction as a big complicated thing, rather than tons of separate, simpler things added together.
Normal waves add together by adding their height. Two crests meet and you get a super crest. Two troughs meet and you get a super trough. Wavefunctions add in the same way, except now because there are arrows instead of heights, you can get arrows that point in the same direction or in opposite directions. Opposite arrows, of equal length cancel, while arrows in the same direction add.
What makes this weird is when you add in probability. Since the probability depends only on the length, if you took two independent states and measured them a bunch of times, you might find that there’s always some chance of finding your particle in a particular spot. Add those states together, however, and the arrows can actually cancel each other out, making the separably possible state now impossible!
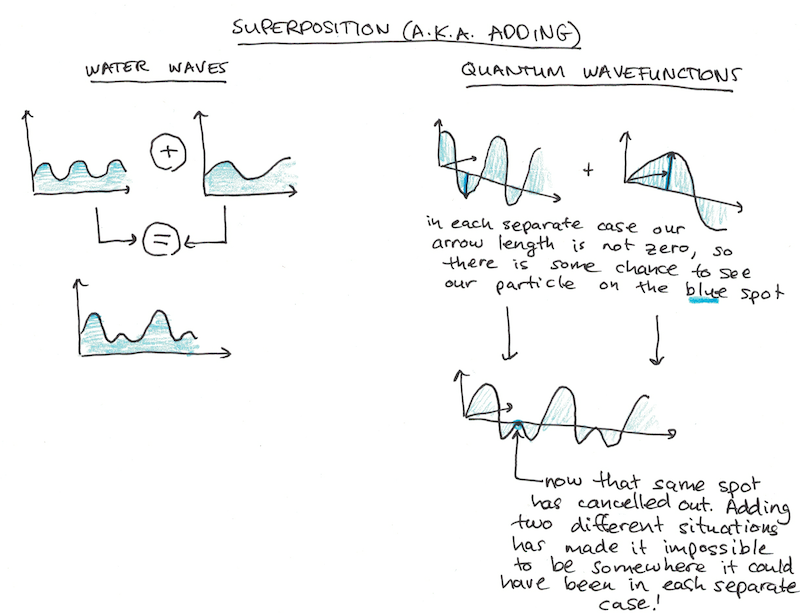
This shows two new and interesting properties of nature:
- That the world is fundamentally random. Not random in the anything-can-possibly-happen variety, but in the kind of randomness you get from playing poker: there’s only some cards that can be drawn (and some you can never draw) but you can’t predict exactly which ones, only the odds.
- That instead of just being a normal probability measure where different possibilities strictly add with each other, quantum mechanics uses arrows instead of values, so by setting a situation up correctly you can make two events which, if done independently, have some chance of happening, completely cancel each other out.
Things Quantum Mechanics Helps Explain
Technically the list of things that quantum mechanics explains needs to include (nearly) all physically observable phenomena, since this is the physical theory everything else, including chemistry, biology, psychology and politics, ultimately reduces to. However, practically speaking, actually calculating the quantum mechanical effects can be intensely difficult, so the actual predictions are more limited.
However, there’s still a lot of phenomena you could observe in everyday life that have a direct and simple explanation from quantum mechanics.
Why Stuff Exists at All
One is simply to explain why there is stuff at all. When scientists discovered the structure of the atom, electrons orbiting nuclei, it was quickly discovered that a classical model wouldn’t work. While it’s still a popular idea to think of the electron to orbit the nucleus like a planet around the sun, there’s an important difference that makes this impossible.
Electrically charged stuff, when it accelerates, gives off light. This is because, classically, a moving charge generates a magnetic field. If the charge is accelerating (meaning changing how fast it is moving) then this generates a changing magnetic field. A changing magnetic field, conversely generates a changing electrical field. These two things couple and become a self-sustaining wave of electromagnetic radiation. We call that wave light.

However, when you give off light, you lose energy. Which means unlike the stable orbits of planets around the sun, a planetary model of the atom has to have the electron rapidly crash into the center of the atom. This means, according to classical mechanics, stuff can only exist for a tiny fraction of a second before collapsing.
If you represent the electron as a wavefunction this problem goes away. Now, however, instead of a wave along a line or a surface, however, it’s each point in 3D space that gets a 2D arrow. Which is harder to visualize, but the math is basically the same. Because the wave has to “sit” in the well created by the nucleus, it has to have a certain minimum energy.
This is a little like how when you pluck a string on a guitar, it produces a certain sound. The frequency of sound corresponds to the waves which match the length of the string. Similarly, a quantum wave has to be the right shape or it can’t “sit” on the atom.
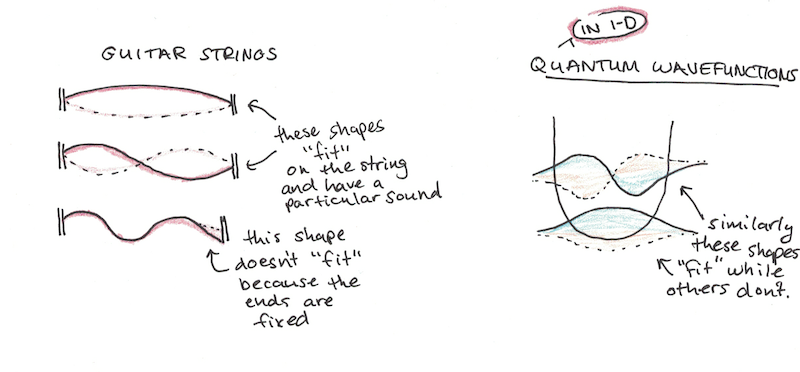
Why The Periodic Table Exists
Even more than allowing stuff to exist, taking the wavefunction for an electron in an atom doesn’t just force a minimum energy, but it forces that the energy levels of the atom be discrete. This is also a surprising fact. Understanding why fully requires knowing differential equations and how complicated states can be broken down into partial wavefunctions of definite energy.
A crude analogy, however, might be to consider our guitar string again. Different waves can resonate on the string, but they are also discrete and based on the length of the string. Waves which don’t fit perfectly onto the length of the string quickly cancel themselves out. Electron wavefunctions are more complicated, so the pattern is more complicated, but it is similarly limited to fit into certain vibrations.
Combining this property, discrete energy levels, with another fact about electrons, that two cannot occupy the same exact state, means that you have atoms with electron orbitals which “fill up” and this explains nearly all of chemistry.
Why Learn Quantum Mechanics
These little bits of trivia may seem like they’re not worth all the work of learning quantum mechanics. But, in my case at least, I think it’s been worth approaching not because of a few facts, but because of how it forces you to think of how reality really is. To paraphrase Richard Feynman, understanding math is necessary to really appreciate the beauty of nature. I think that is worth the effort.


 I'm a Wall Street Journal bestselling author, podcast host, computer programmer and an avid reader. Since 2006, I've published weekly essays on this website to help people like you learn and think better. My work has been featured in The New York Times, BBC, TEDx, Pocket, Business Insider and more. I don't promise I have all the answers, just a place to start.
I'm a Wall Street Journal bestselling author, podcast host, computer programmer and an avid reader. Since 2006, I've published weekly essays on this website to help people like you learn and think better. My work has been featured in The New York Times, BBC, TEDx, Pocket, Business Insider and more. I don't promise I have all the answers, just a place to start.