Book Review: Human Problem Solving

How do we solve hard problems? What are we thinking about as we work? What influences whether we find an answer or remain stuck forever?

These are the questions Allen Newell and Herbert Simon set out to address in their landmark 1972 book, Human Problem Solving. Their work has had an enormous influence on psychology, artificial intelligence, and economics.

How do you get reliable data for complicated problems? Here’s the basic strategy behind HPS:

1. Find a category of problems you want to study.¹
2. Write a computer program to solve the problem.
3. Get participants to solve the problem while verbalizing their thought processes.
4. Compare the computer program to the transcripts of real people solving the problem and look for similarities and differences.

While all models are imperfect, computer programs have some distinct advantages as theories of human performance. For starters, they can solve the problems proposed. Since we know how computers work, but not how minds work, using a known process—the computer program—as a model avoids the issue of trying to explain one mysterious phenomenon with another.

However, Newell and Simon go further than this theoretical convenience. They argue that human thinking is an information processing system, just as a computer is. This remains a controversial thesis, but nonetheless, it makes strong and interesting predictions about how we think.²

Key Idea: Problem Solving is Searching a Problem Space

Newell and Simon argue problem solving is essentially a search through an abstract problem space. We navigate through this space using operators, and those operators transform our current information state into a new one. We evaluate this state, and if it matches our answer (or is good enough for our purposes), the problem is solved.

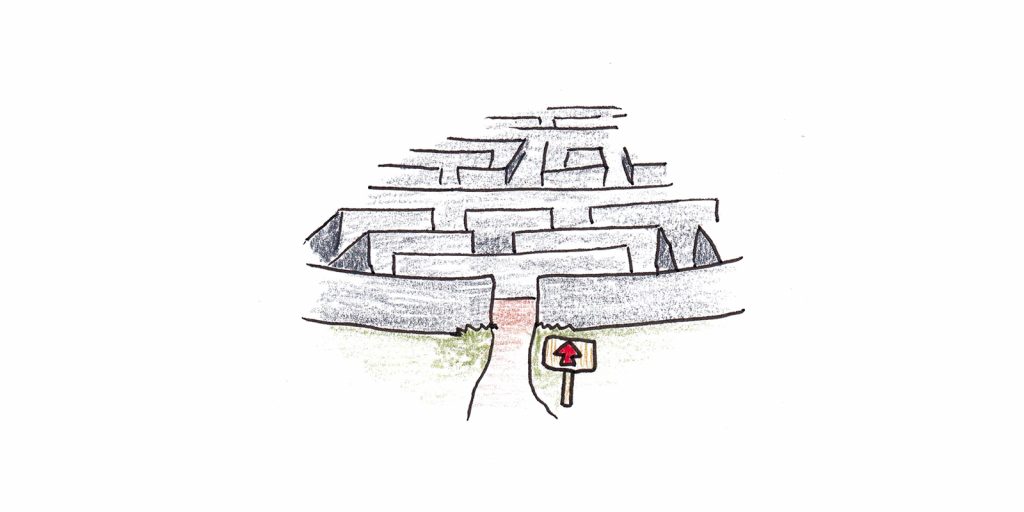
We can liken this to finding our way in a physical space. Compare problem solving to finding the exit of a maze:

• The problem space is the physical space in the maze. You have some current location, and you want to be at the exit. Solving the problem means finding your way out.
• Operators are the physical movements you can make. You can go left, right, forward or backward. After each movement, you’re in a different place. You evaluate your new state and decide if you have found the solution or if you should move again.

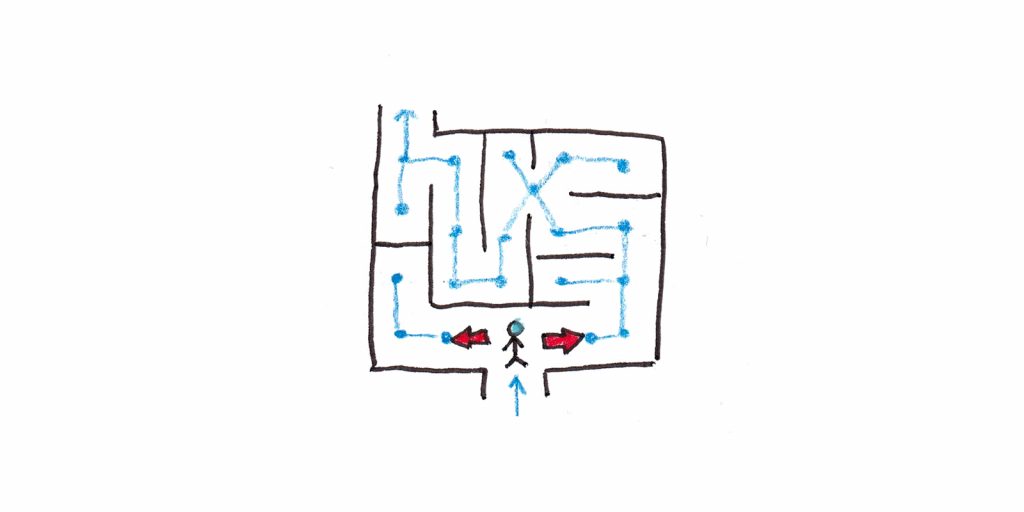
Now consider solving a Rubik’s Cube. How does this perspective on problem solving apply?

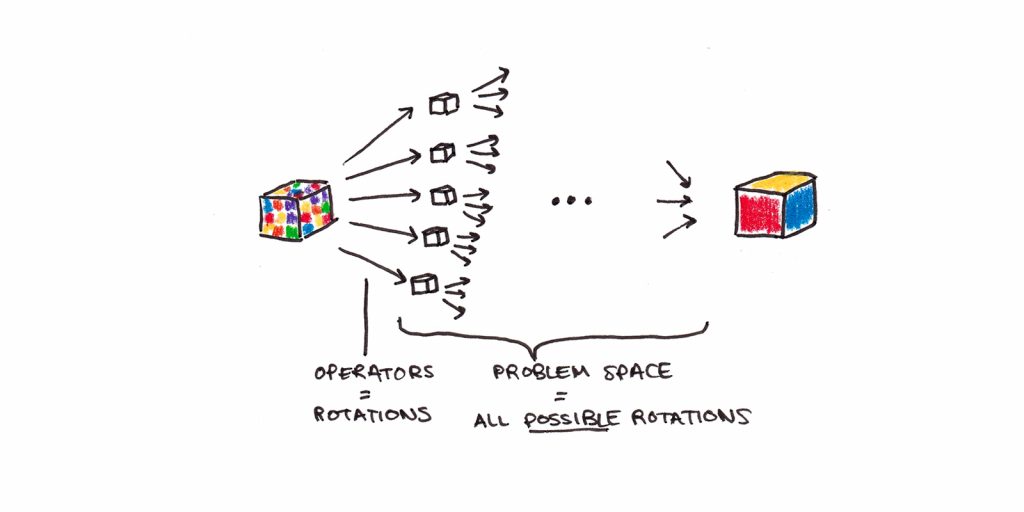
• The problem space is all the possible configurations of the cube. Given there are over 43 quintillion possibilities, the space is enormous.
• The operators are your ability to rotate the cube in various directions. Even though the space is vast, the operators available at each moment are quite limited.
• Solving the puzzle involves moving through this abstract problem space, ending in a configuration where the colors are properly segregated to each side of the cube.

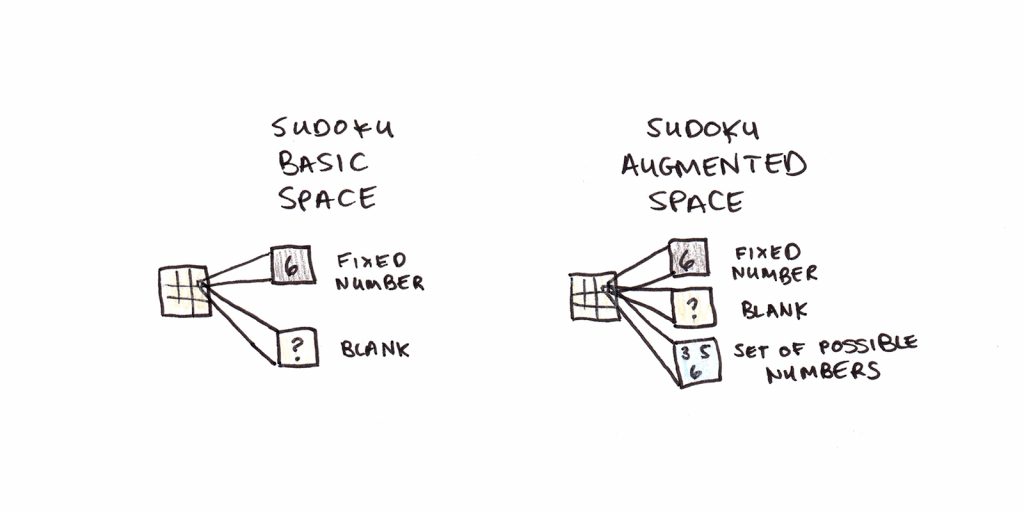
In a Rubik’s Cube, the operators on the problem space are physical, but they need not be. Consider Sudoku, where there might be other ways of conceptualizing the problem, resulting in different problem spaces:

• A basic space might just be the set of all possible assignments of numbers to squares. Most of these would fail to fit the constraints of the numbers 1-9 being used uniquely in each subgrid, row, and column. Search in this space might look like trying out a random combination and seeing if it is correct.
• A better space would be augmented. Instead of allowing only fixed numbers at each square, you might have information about sets of “possible” numbers. Operators would consist of fixing a particular square and eliminating possibilities from those that remain via other constraints. This is closer to how experts solve Sudoku puzzles, as the basic problem space is unwieldy.

The difficulty of solving a problem isn’t always in searching the problem space. Sometimes, the hard part is choosing the correct space to work in in the first place. Insight-based puzzles, such as the nine-dot puzzle, fit this pattern. In this puzzle, you must cross all nine dots using four straight lines, drawn without lifting your pencil from the paper.

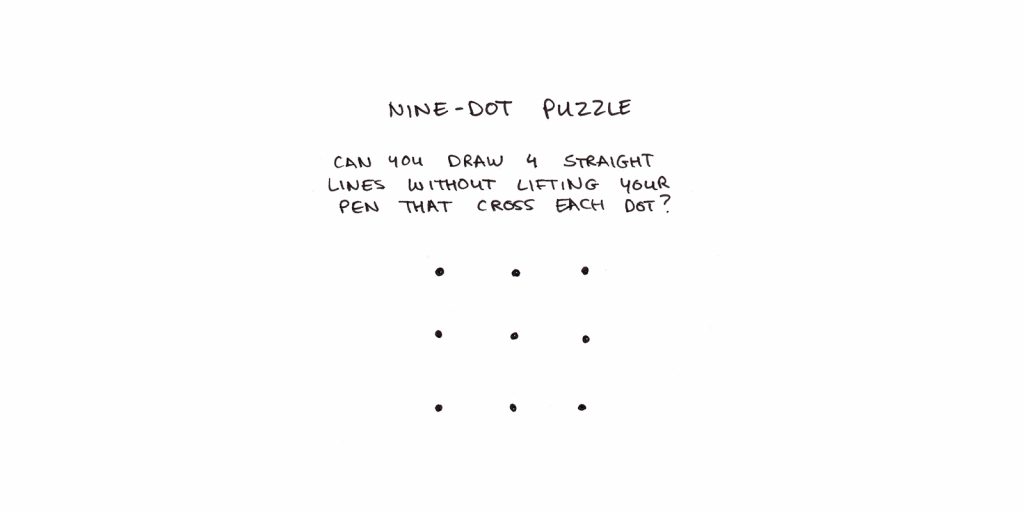
What makes this puzzle difficult is finding the problem space where the solution exists. (Answer here for those interested.)

What Determines Problem Solving Difficulty?

I’ve already mentioned two factors that influence the difficulty of problems: the size of the problem space and how strongly the task itself suggests the best space. Newell and Simon found others in their research.

A simple one is the role memory has on problem solving. Human cognition depends far more on memory than most of us realize. Because working memory is limited, we lean heavily on past experience to solve new problems.

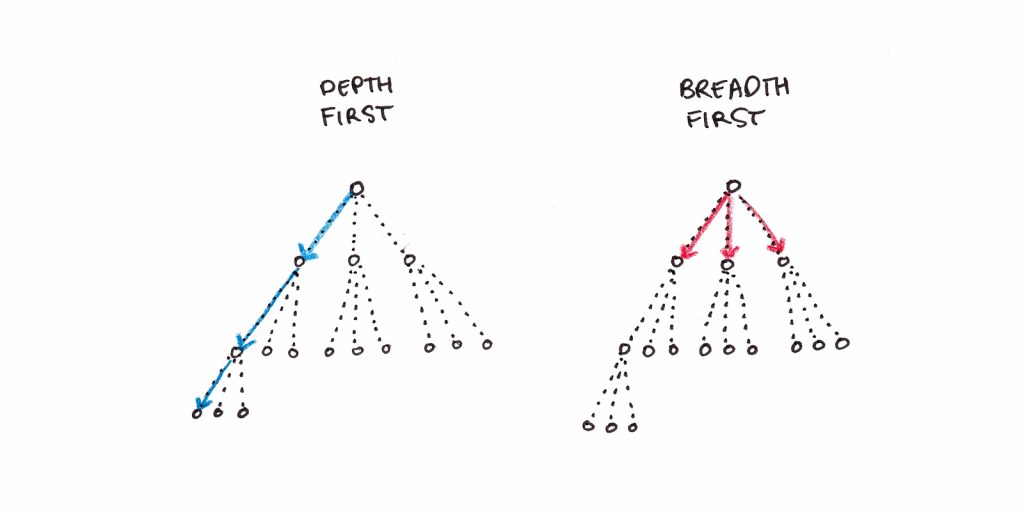
For instance, subjects universally prefer evaluating chess positions one sequence of moves at a time rather than pursuing multiple sequences simultaneously. For computers, the difference between breadth-first and depth-first search is a technical choice. For humans, depth-first is necessary because we don’t have the working memory capacity to hold multiple intermediate positions in our mind’s eye.

Conversely, many problems cease to be problems at all once we have the correct procedure in memory. As we learn new things, we develop memorized answers and algorithms that eliminate the need for problem solving altogether. Tic-tac-toe is a fun puzzle when you’re a kid, but it’s boring as an adult because the game always leads to a stalemate.

To see something as a problem, then, means it must occupy a strange middle-ground. It must be unfamiliar enough so that the correct answer is not routine, yet not so vast and inscrutable that searching the problem space feels pointless.

Is There a Programming Language of Thought?

Given Newell and Simon frame their theories of human cognition in terms of computer programs, this raises a question: what sorts of programs fit best?

Newell and Simon argue in favor of production systems. A production system is a collection of IF-THEN patterns, each independent from one another. The collection of productions fires when the “IF” part of the observed pattern matches the contents of short-term memory. The “THEN” part corresponds to an operator—you do something to move yourself through the problem space.

This remains a popular choice. ACT-R theory, which continues to be influential in psychological research, is also based on the production system framework.

Productions have a few characteristics that make them plausible for modeling aspects of human thought:

• Their modularity means that parts of what has been learned can transfer to new skills. While transfer research has often been pessimistic, it’s clear that humans transfer acquired skills much better than most computer programs.
• They extend the basic behaviorist notions of stimulus-response. Productions are like habits except, because they can operate on both internal and external states, they are far more powerful. They can incorporate goals, desires and memories.
• They force serial order on human thinking. The brain’s underlying architecture is massively parallel—billions of independently firing neurons. But human thinking is remarkably serial. Productions, processed in parallel but acted on in sequence, suggest a resolution to the paradox.

Can We Solve Problems Better?

Human Problem Solving articulates a theory of cognition, not practical advice. Yet it has implications for the kinds of problems we face in life:

1. The Power of Prior Knowledge

Prior knowledge exerts an enormous influence on problem solving. While raw intelligence—often construed as processing speed or working memory capacity—does play a role, it is often far less important than having key knowledge.

Consider the ways prior knowledge influences your thinking:

• Prior knowledge determines your choice of problem space. This is clear in the cryptarithmetic puzzles used by Newell and Simon. Subjects who already knew a lot about multi-digit addition were able to form a problem space consisting of letter values, odd-even parities and carries. In contrast, less-knowledgeable subjects struggled. Some worked in a more basic problem space, trying out random combinations before giving up. Others attempted dozens of different problem spaces, none of which were particularly suited to the task.
• Prior knowledge determines which operators are available to you. A sophisticated library of operators can make the problem much easier to solve. In some cases, it can eliminate the problem entirely as search is no longer required—you simply proceed with an algorithm that gets the answer directly. Much of what we do in life is routine action, not problem-solving.
• Prior knowledge creates memories of specific patterns, reducing analysis required. In chess, for instance, dynamic patterns require a player to simulate how play will unfold over time. This difficult-to-process task can be replaced by learning static patterns whose outcomes are understood just by looking at them. Consider a pattern such as a “forking attack” where a knight attacks two pieces simultaneously. While this pattern can be discovered through searching the possible future moves of the pieces in play, good players recognize it visually on the board. Simple recognition eliminates the need to formally analyze the implications of each piece, sparing precious working memory capacity.

All of this suggests that knowledge is more important than intelligence for particular classes of problems. Of course, the two factors are often correlated. Intelligence speeds learning, which allows you to have more knowledge. However the intelligence-as-accelerated-knowledge-acquisition picture suggests different implications than the intelligence-as-raw-insight picture we often associate with genius. Geniuses are smart, in large part, because they know more things.

2. The Only Solvable Problems are Tractable Ones

This is an area where I’ve changed my thinking. Previously, I had written about what I called “tractability bias.” We tend to work on solvable, less important problems rather than harder problems that don’t suggest any solutions.

There is some truth to this account: we do tend to avoid impossible-seeming problems, even if they’re more worthy of our efforts. Yet HPS points to an obvious difficulty: the importance of a problem has nothing to do with our ability to solve it. Even for well-defined challenges, problem spaces can be impossibly vast. Finding a solution, even something that is “good enough,” can be impractical for many classes of problems.

I suspect our emotional aversion to hard problems comes from this place. Unless we have reasonable confidence our problem solving search will arrive at an answer we don’t invest any effort. Because the size of problem spaces can often be enormous, this is shrewd, not lazy.

To be successful we need to work on important problems. But, we also need to find ways to make those problems tractable. The intersection of these two requirements is what makes much of life so intriguing—and challenging.

1. HPS focuses on three: cryptarithmetic puzzles, logic theorem proving and chess.
2. For some rebuttals to this position, consider Hubert Dreyfus, Philip Agre and Jean Lave. Note also counter-rebuttals from Herbert Simon and John Anderson.